Big Data demais: lidando com a plotagem excessiva

Com todo o hype em torno do Big Data nos últimos anos, é fácil supor que ter mais dados é sempre uma vantagem. Mas, à medida que adicionamos mais e mais pontos de dados a um gráfico de dispersão, podemos começar a perder esses padrões e clusters. Esse problema, resultado de plotagem excessiva, é demonstrado na animação abaixo.

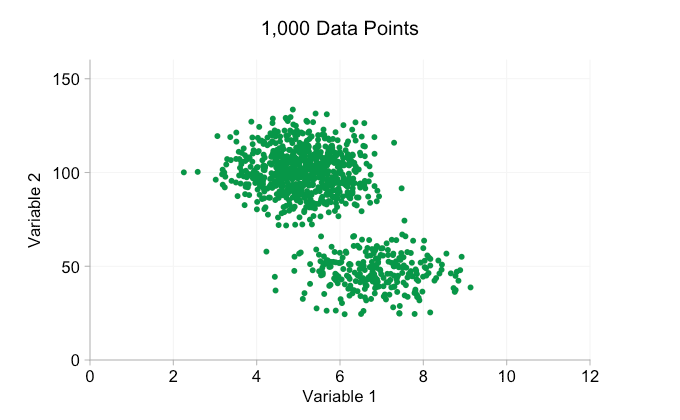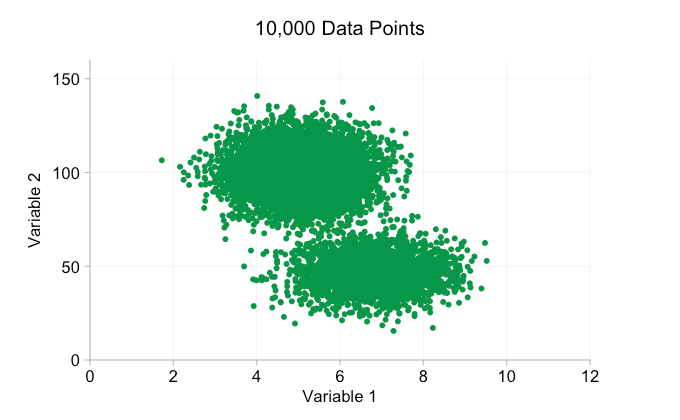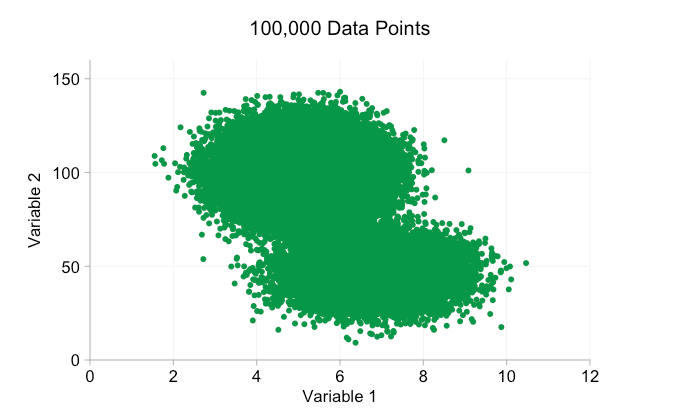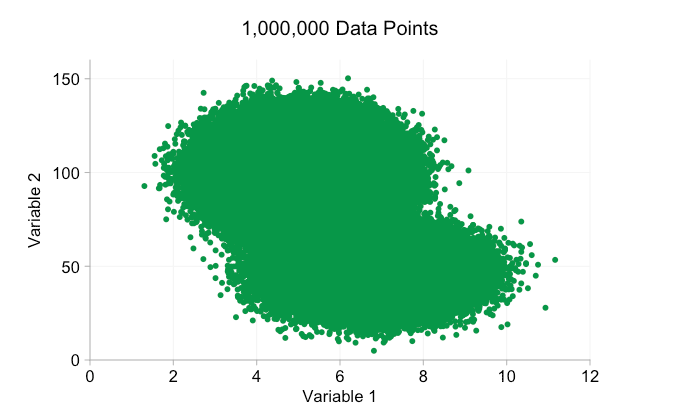
Os dados na animação acima são gerados aleatoriamente a partir de um par de distribuições bivariadas simples. A distinção entre as duas distribuições torna-se cada vez menos clara à medida que adicionamos mais e mais dados. Então, o que podemos fazer sobre a sobrecarga?

Uma opção simples é diminuir os pontos de dados. (Observe que esta é uma "solução" ruim se muitos pontos de dados compartilharem exatamente os mesmos valores.) Também podemos torná-los semitransparentes. E podemos combinar essas duas opções:

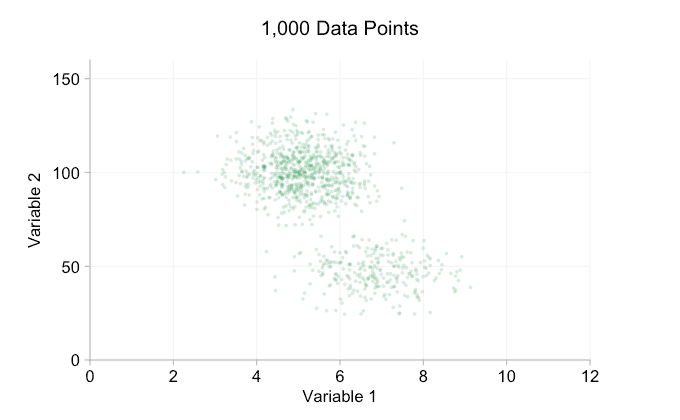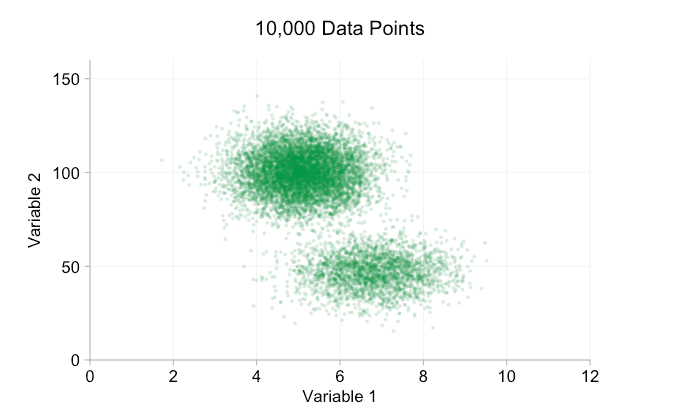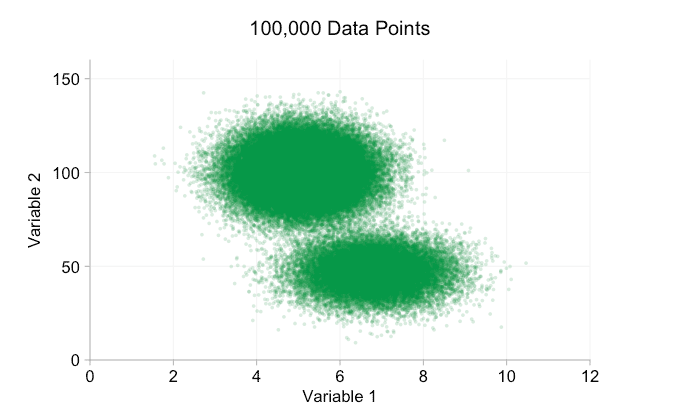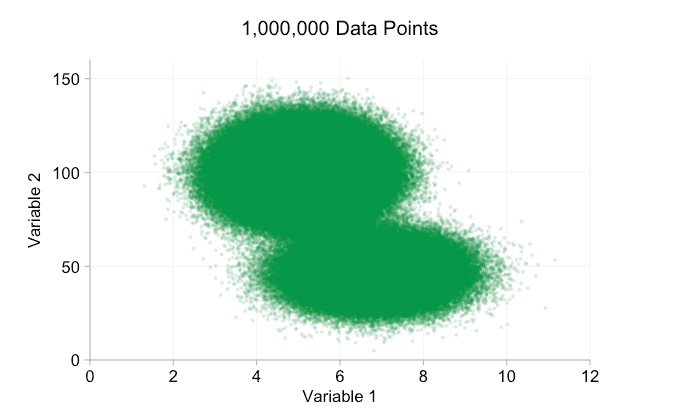
Esses refinamentos certamente ajudam quando temos dez mil pontos de dados. No entanto, quando atingimos um milhão de pontos, as duas distribuições aparentemente se fundiram em uma novamente. Tornar os pontos menores e mais transparentes pode ajudar as coisas; No entanto, em algum momento, podemos ter que considerar uma mudança de visualização. Falaremos disso mais tarde. Mas primeiro vamos tentar complementar nossa visualização com algumas informações extras. Especificamente, vamos visualizar as distribuições marginais. Temos várias opções. Há muitos dados para um gráfico de tapete, mas podemos descartar os dados e mostrar histogramas. Ou podemos usar uma opção mais suave – um gráfico de densidade de kernel. Finalmente, poderíamos usar a distribuição cumulativa empírica. Esta última opção evita qualquer binning ou suavização, mas os resultados são provavelmente menos intuitivos. Vou usar a opção de densidade do kernel aqui, mas você pode preferir um histograma. O gif animado abaixo é o mesmo que o gif acima, mas com as distribuições marginais suavizadas adicionadas. Deixei as escalas desativadas para evitar desordem e porque só estamos realmente interessados em julgamentos aproximados de altura relativa.

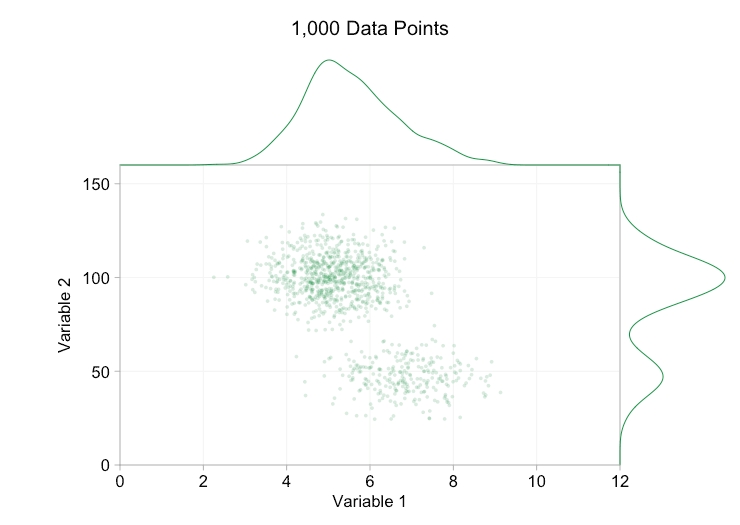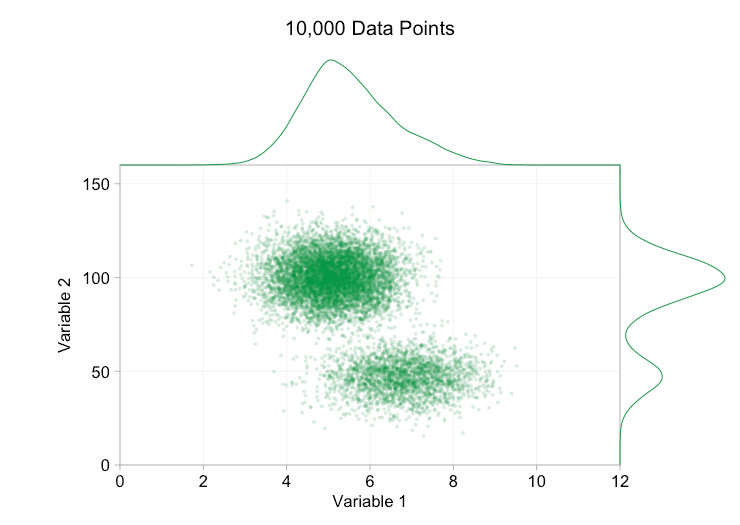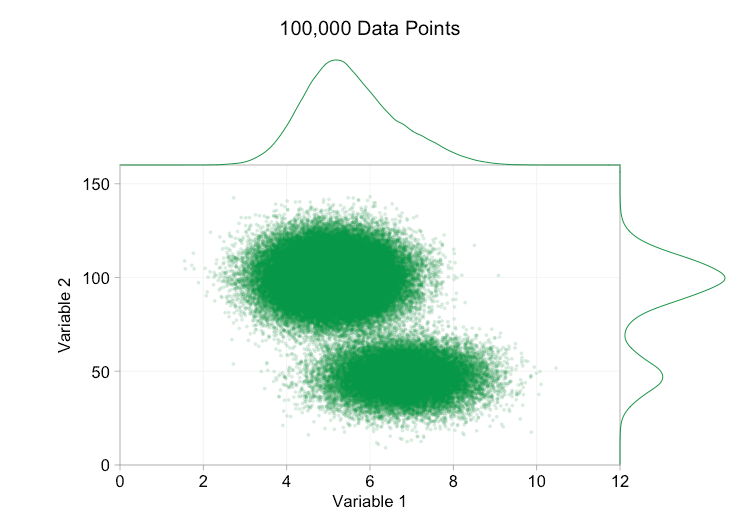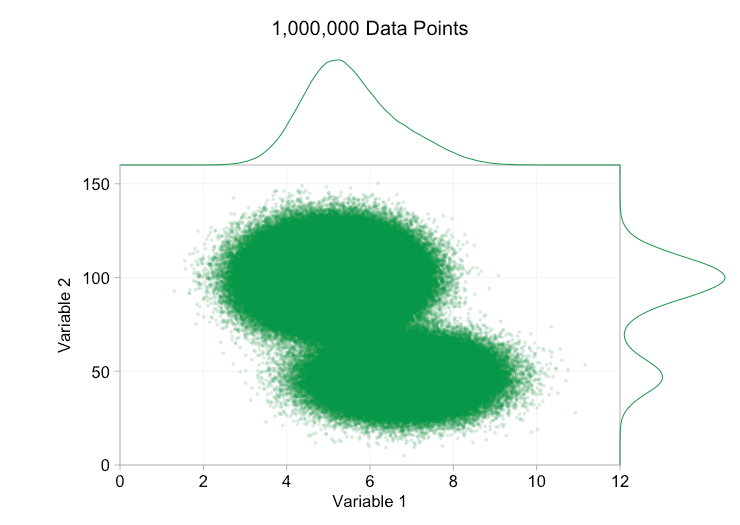
A adição de distribuições marginais, particularmente a distribuição da Variável 2, ajuda a esclarecer que duas distribuições diferentes estão presentes nos dados bivariados. A natureza de pico duplo da Variável 2 é evidente se há mil pontos de dados ou um milhão. Os tamanhos relativos dos dois componentes também são claros. Por outro lado, a distribuição marginal da Variável 1 tem apenas um único pico, apesar de vir de duas distribuições distintas. Isso deve deixar claro que a adição de distribuições marginais não é de forma alguma uma solução universal para a plotagem excessiva em gráficos de dispersão. Para reforçar esse ponto, a animação abaixo mostra um conjunto completamente diferente de pontos de dados (gerados) em um gráfico de dispersão com distribuições marginais. Os dados novamente vêm de uma amostra aleatória de duas distribuições 2D diferentes, mas ambas as distribuições marginais do conjunto de dados completo não destacam essa separação. Como anteriormente, quando o número de pontos de dados é grande, a distinção entre os dois clusters também não pode ser vista no gráfico de dispersão.

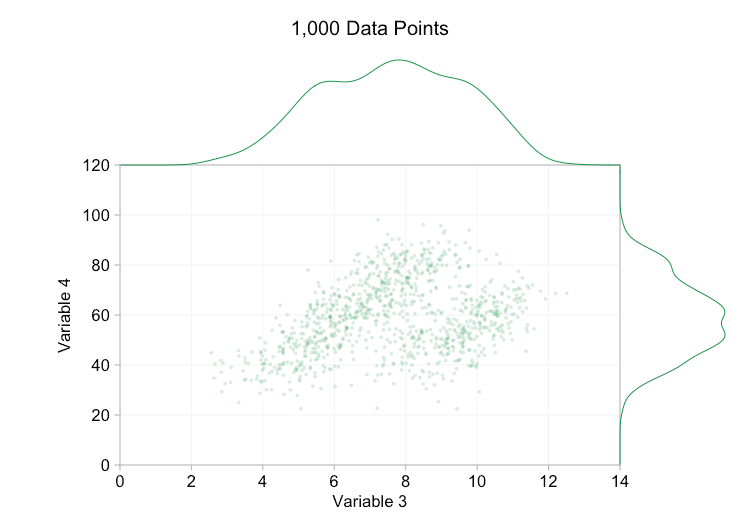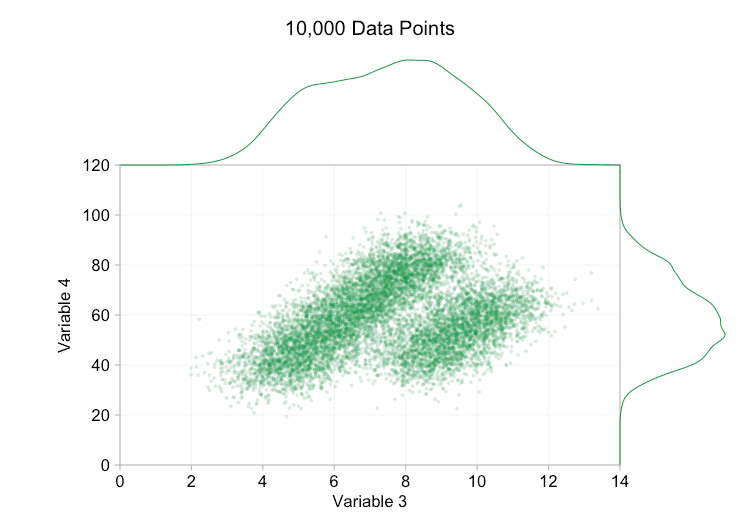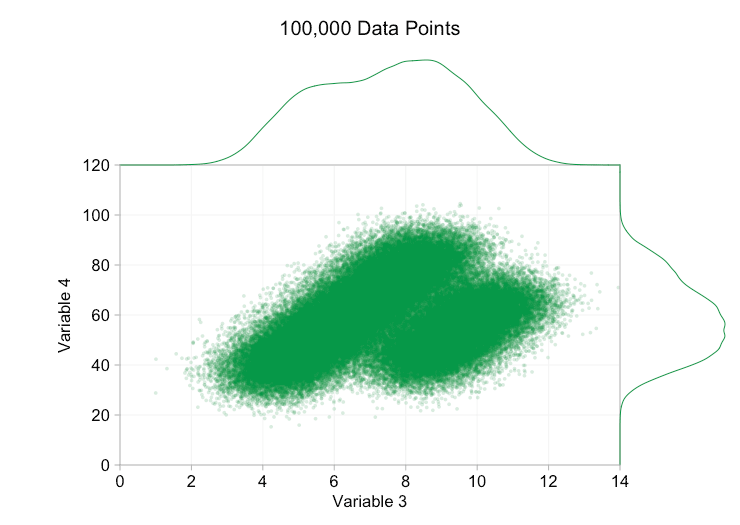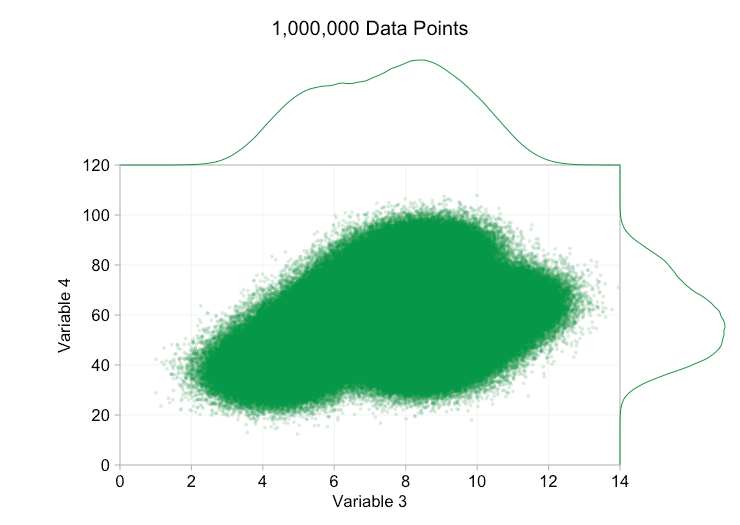
Voltando ao tamanho e à opacidade do ponto, o que obtemos se tornarmos os pontos de dados muito pequenos e quase completamente transparentes?

Agora podemos distinguir claramente dois clusters em cada conjunto de dados. É difícil distinguir qualquer detalhe.

Como perdemos esse detalhe de qualquer maneira, parece adequado questionar se realmente queremos desenhar um milhão de pontos de dados. Pode ser tediosamente lento e impossível em certos contextos. Os histogramas 2D são uma alternativa. Ao agrupar dados, podemos reduzir o número de pontos a serem plotados e, se escolhermos uma escala de cores apropriada, escolher alguns dos recursos que foram perdidos na desordem do gráfico de dispersão. Depois de algumas experiências, escolhi uma escala de cores que ia do preto ao verde e ao branco na extremidade alta. Observe que isso é (quase) o inverso do efeito criado pela sobreplotagem nos gráficos de dispersão acima.

Em ambos os histogramas 2D, podemos ver claramente os dois clusters diferentes que representam as duas distribuições das quais os dados são extraídos. No primeiro caso, também podemos ver que há mais contagens do cluster superior esquerdo do que do cluster inferior direito, um detalhe que se perde no gráfico de dispersão com um milhão de pontos de dados (mas mais óbvio nas distribuições marginais). Por outro lado, no caso do segundo conjunto de dados, podemos ver que as "alturas" dos dois clusters são aproximadamente comparáveis.

Os gráficos 3D são usados em excesso, mas aqui (veja abaixo) acho que eles realmente funcionam muito bem em termos de fornecer uma visão ampla de onde os dados estão e não estão concentrados. A oclusão de recursos é um problema com gráficos 3D, portanto, se você for seguir esse caminho ao explorar seus próprios dados, recomendo usar um software que permita a interação do usuário por meio de rotação e zoom.

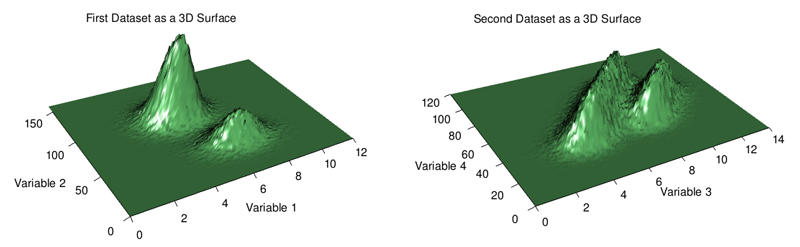
Em resumo, os gráficos de dispersão são uma maneira simples e muitas vezes eficaz de visualizar dados bivariados. Se, no entanto, seu gráfico sofrer de plotagem excessiva, tente reduzir o tamanho e a opacidade do ponto. Caso contrário, um histograma 2D ou mesmo um gráfico de superfície 3D pode ser útil. Neste último caso, tenha cuidado com a oclusão.